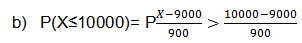Propiedades de la esperanza

El valor esperado de una variable aleatoria E(x) es un parámetro de centralización y su significado es similar al de la media aritmética de un conjunto de datos. Las propiedades presentadas a continuación son correctas para las variables continuas y discretas.

Las propiedades del valor esperado son validas tanto para variables discretas como continuas.

1)    El valor esperado de una constante es igual a ella misma E(C) = C, siendo C una constante.

 Ejemplo:

Si la constante es el numero 5, E(5)=5

2)    Si A y B son variables aleatorio se cumple que:

E(X + Y) = E(X) + E(Y)

Esto indica que el valor esperado de la suma de dos variables aleatorias es igual a la suma de sus valores esperados.

Ejemplo:

X	0	1	2
P(X=x)	1/8	3/8	1/8
	0,125	0,375	0,125

E(x): [(0*0,125) + (1*0,125) + (2*0,125)]

E(x): [ 0 + 0,125 + 0,25)

E(x): 0,375

Y	0	1	2	3
P(Y=y)	3/4	1/4	2/4	1/4
	0,75	0,25	0,5	0,25

E(y): [(0*0,75) + (1*0,25) + (2*0,5) + (3*0,25)]

E(y): [ 0 + 0,25 + 1 + 0,75)

E(y): 2

Entonces E(X+Y)=  0,375 + 2 = 2,375

3)    El valor esperado del producto de una constante por una variable aleatoria, es igual al producto de la constante por el valor esperado de la variable:

E(C*X)=C*E(X)

Ejemplo:

Ejemplo: Dados C= 2 y E(X)= 0,375

E(C.X)= 2. 0,375

E(C.X)=0,75

4)    Si X es una variable aleatoria e Y es otra variable aleatoria, el valor esperado del producto de las variables es igual al producto de los valores esperados, solamente en el caso de que las variables X e Y sean independientes.

                                                   E(X.Y)= E(X). E(Y)

Ejemplo. Dado E(X)= 0,375, E(Y)= 2

E(X.Y)= 0,375 * 2

E(X.Y)= 0,75

Propiedades de la varianza

            1)    La varianza de una constante es cero, la varianza mide la dispersión, evidentemente              una constante no puede tener dispersión por lo tanto su varianza es cero.

Var (C) = 0

Ejemplo.

Dado X{3}, E(X)=3 y P(X)=0,375

Hallar la varianza:

Var(X)= (3 – 3 )² * 0,375

Var(X)= 0

            

             2)    La varianza del producto de una constante por una variable, es igual a la constante                al cuadrado por la varianza de la variable.

Var (CX) = C² Var (X)

Ejemplo:

Dado el valor de C= 8

Var(X)= [((0-1,12)² * 0,2) + ((1-1,12)² * 0,04) + ((2 – 1,12)² * 0,04) + ((3 – 1,12)² * 0,1)]

Var(X)= 0,2508 + 0,0005 + 0.0309 + 0,3534

Var(X)= 0,6356

Var(C.X)= 8². 0,6356

Var(C.X)= 64 * 0,6356

Var(C.X)= 40,6784

              3)    Si  X e Y son variables aleatorias cualesquiera:

                                   Var(X+Y)= Var(X)+Var(Y)

La varianza de la suma de dos variables independientes es igual a la suma de las               varianzas.

   

     Ejemplo.

    Dado Var(X)= 0,3611

-               Hallamos la varianza Y

   Var(Y)= [((0 – 0,17)² * 0,9) + ((1 - 0,17)² * 0,06) + ((2 – 0,17)² * 0,02) +((3 – 0,17)² * 0,01)]

   Var(Y)= (0,026 + 0,041 + 0,066 + 0,080)

   Var(Y)=0,213

   Var(X+Y)=0,3611+0,213

   Var(X+Y)=0,5741

Propiedades de la desviación estándar

Dado que la varianza tiene sus unidades originales elevadas al cuadrado, se define la desviación estándar como:

       1)    La varianza de una constante es cero, la varianza mide la dispersión, evidentemente una constante no puede tener dispersión por lo tanto su varianza es cero.

Var (C) = 0

Ejemplo.

Dado X{3}, E(X)=3 y P(X)=0,375

Hallar la varianza:

Var(X)= (3 – 3 )² * 0,375

Var(X)= 0

    DE (X)= 0

       2)    La varianza del producto de una constante por una variable, es igual a la constante al cuadrado por la varianza de la variable.

Var (CX) = C² Var (X)

Ejemplo:

Dado el valor de C= 8

Var(X)= [((0-1,12)² * 0,2) + ((1-1,12)² * 0,04) + ((2 – 1,12)² * 0,04) + ((3 – 1,12)² * 0,1)]

Var(X)= 0,2508 + 0,0005 + 0.0309 + 0,3534

Var(X)= 0,6356

Var(C.X)= 8². 0,6356

Var(C.X)= 64 * 0,6356

Var(C.X)= 40,6784

 DE (X)= 6,3779

      3)    Si  X e Y son variables aleatorias cualesquiera:

                                   Var(X+Y)= Var(X)+Var(Y)

La varianza de la suma de dos variables independientes es igual a la suma de las varianzas.

Ejemplo.

Dado Var(X)= 0,3611

-       Hallamos la varianza Y

Var(Y)= [((0 – 0,17)² * 0,9) + ((1 - 0,17)² * 0,06) + ((2 – 0,17)² * 0,02) +((3 – 0,17)² * 0,01)]

Var(Y)= (0,026 + 0,041 + 0,066 + 0,080)

Var(Y)=0,213

Var(X+Y)=0,3611+0,213

Var(X+Y)=0,5741

 DE (X)= 0,7576

                   Las Distribuciones de Probabilidad en Ciencias de la Salud

Como es de conocimiento evidente, la parte de probabilidades en el área de la salud es un tema de interés, ya que puede servir de base al momento de realizar diagnósticos, toma de decisiones, en lo que respecta a diversos aspectos como la administración de tratamientos, uso de equipos o exámenes paraclínicos; entre otros, en el afán por la búsqueda de realizar diagnósticos acertados o por lo menos tratamientos que sea lo más idealizados posible al paciente, para curar o mejorar la condición del paciente, tomando en cuenta que cada organismo es diferente y no siempre reacciona de la misma manera.

Es aquí donde radica la importancia que tiene la elaboración de pruebas, experimentos, ensayos entre otros métodos que sirvan y le proporcionen al personal de salud más pistas, debido a que generalmente la sintomatología de una enfermedad puede ser similar a otra o puede variar con síntomas totalmente distintos en pacientes con la misma condición. Pero no solo enfocándose en diagnóstico de patologías sino que también es utilizada en prevención y planificación, pues permite hacer una previsualización de lo que podría pasar. Generalmente se relaciona a publicaciones demográficas, económicas y sociológicas llevadas a cabo anteriormente, gran parte de los resultados de la estadística provienen de la curiosidad de ciertas personas por desarrollar modelos que expresen el comportamiento de ciertos aspectos de la materia y de los caracteres biológicos o humanos para la mayoría de los casos. Por ejemplo la medicina, la biología, la física, la psicología, patología, ortopedia, en fin, casi todos los campos de las ciencias emplean herramientas estadísticas fundamentales para el desarrollo de sus patrones de trabajo.

Seguidamente se presentan ejemplos de algunas distribuciones de probabilidad.

           a)    Experimento de Bernoulli

Una persona femenina de 20 años de edad se realiza una prueba elisa de cuarta generación para diagnosticar si padece o no del virus de VIH. Considerando el resultado de la prueba positivo como un fracaso (F) y negativo como un éxito (E).

           b)    Experimento Binomial

Se realiza un estudio de aspirado de médula ósea en 8 pacientes con edades comprendidas entre 10 y 13 años para diagnosticar la presencia de un cáncer en la sangre. Se considera el resultado positivo como un fracaso (F) y el resultado negativo como un éxito (E).

           c)    Distribución Binomial

Se sabe que el 35% de los pacientes que asisten a una consulta de oftalmologia poseen miopia. Determinar la probabilidad de que una muestra aleatoria de 6 personas:

a.- Mas de 5 posean miopia

b.- 1 tenga miopía

X(n=6; p=0,35)

La probabilidad de que más de 5 pacientes posean miopía es de 0.0367

La probabilidad de que más de 1 pacientes posean miopía es de 0.2436

d)    Distribución normal estandarizada

    El salario mensual de un médico cardiólogo infantil de la unidad de pediatria en el IAHULA sigue una distribución normal con μ=9000 Bs y σ=900 Bs. Se pide:

a) La probabilidad de que el salario mensual de un médico cardiólogo infantil de la unidad de pediatría en el IAHULA sea superior a 12000 BsF.

b) La probabilidad de que el salario mensual de un médico cardiólogo infantil de la unidad de pediatría en el IAHULA sea inferior a 10000 BsF.

Sea X {salario mensual de un médico cardiólogo infantil de la unidad de pediatría en el IAHULA}

Z= (µ=9000; σ=900)

P(Z≥3,33)= 1 - P(Z≤3,33)= 1 – 0,9996= 0,0004

La probabilidad de que el salario mensual de un médico cardiólogo infantil de la unidad de pediatría en el IAHULA sea superior a 12000bsf es de 0,0004. Esto indica que es un evento poco probable.

P(Z≤1,11)=0,8665

La probabilidad de que el salario mensual de un médico cardiólogo infantil de la unidad de pediatría en el IAHULA sea inferior a 10000bsf es de 0,8665.

Chi-Cuadrado

a.- P(X²≤0,95) con 7 grados de libertad= 2,17

El valor de la variable X² que deja a su izquierda, un área de 0,95 0 95% en una distribución con 7 grados de libertad es de 2,17

b.- P(X²≥0,80) con 10 grados de libertad= P(X²≤0,20)=13,44

El valor de la variable X² que deja a su derecha, un área de 0,80 u 80% en una distribución con 10 grados de libertad es de 13,44

c.- P(0,10≤X²≤ 0,70) con 4 grados de libertad= 7,78≤ X²≤2,20

El valor de la variable X² que deja a su izquierda, un área de 0,10 0 10% en una distribución con 4 grados de libertad es de 7,78; mientras que el valor a la derecha deja un área de 0,70 o 70% es de 2,20.

T-Studens

Dada una variable t de Student con 20 grados de libertad. Hallar el valor de t que deja un área total de 5% en ambos extremos.

Usando la tabla α=0,025 se tiene que t=2,0860 para la cola derecha y debido a la simetría de la distribución de t, el valor de la cola izquierda es el mismo pero con signo contrario, es decir, t=-2,0860

Plantear un problema de salud donde se aplique la probabilidad.

Problema 1:

 Se realizó un experimento en 5 estudiantes de post-grado de cirugía en el IAHULA Mérida- Venezuela, cuatro pacientes femeninos y un paciente masculino, para conocer la intolerancia al látex usado como materia prima en la elaboración de guantes quirúrgicos.

Pacientes femeninos: 
F1: SI / NO

F2: SI / NO 

F3:  SI / NO 

F4:  SI / NO 

Pacientes masculino: 
M1: SI / NO

Hallo el espacio muestral:
S:{F1SI, F1NO, F2SI, F2NO, F3SI, F3NO, F4SI, F4NO, M1SI, M1NO}

Hallo evento 1:
a) El resultado del experimento sea que todos los pacientes sean alérgicos.

E1: {FISI, F2SI, F3SI, F4SI, M1SI}


Hallo la probabilidad: 
P=5/10=0.5

Interpretación: la probabilidad de que el resultado del experimento sea que todos los pacientes sean alérgicos es de 0.5.

Hallo evento 2:

b) El resultado del experimento sea que las pacientes femeninas NO sean alérgicas.

E2: {F1NO, F2NO, F3NO, F4NO}

Hallo la probabilidad: 
P=4/10=0.4

Interpretación: la probabilidad de que el resultado del experimento sea que las pacientes femeninas no sean alérgicas es de 0.4.

     Este experimento presentado es aleatorio ya que se conocen todos los posibles resultados del experimento realizado. 

 Relación entre probabilidad y salud

La probabilidad relacionada con las ciencias de la salud, se usa como una estrategia mediante la cual se intenta estimar la frecuencia con la que se obtiene un cierto resultado en estudios en donde se tienen todas las variables y resultados. La probabilidad ha permitido establecer resultados fidedignos en cuanto a la eficacia de un fármaco, tratamientos, diagnósticos, prevalencia de enfermedades.

       En las ciencias de la salud la probabilidad ayuda a crear planes preventivos, en cuanto a la frecuencia de aparición de una enfermedad, por ejemplo, si se tiene la variable “ingesta de grasas” se aumenta la probabilidad de sufrir enfermedades a nivel de las arterias coronarias. Por otro lado si la variable es “alimentación balanceada” aumenta la probabilidad de una vida sana prolongada.

            También podemos asociar la probabilidad con respecto a el diagnostico que se le realiza a un paciente, obteniendo signos anormales que puedan referirse a una enfermedad, por ejemplo; si se le realiza una auscultación del corazón a un paciente y se detecta un soplo sistólico, según estudios realizados previamente, probablemente se estaría en presencia de una cardiopatía. Sí se relaciona la probabilidad con el tratamiento, hoy en día se aplican las técnicas que en estudios posteriores han arrojado resultados positivos para el paciente.

            Por último, la probabilidad es muy importante en el trabajo diario del profesional en la ciencia de la salud ya que permite emplear los métodos mas adecuados y efectivos para obtener los mejores resultados. 

RESUMEN: UNA MIRADA A LA ESTADÍSTICA 

En la medicina y otras ciencias de la salud y biomédicas se busca es un grado de certeza de los tratamientos que se implementaran con los pacientes ya sean para recuperar la salud o conservarla incluso también para prevenir la enfermedad. Es por ello que la información que arroja las estadísticas influyen en la confianza que se le otorga a un determinado tratamiento o también nos da una certeza de cuando no va a funcionar y eso ayuda a la toma de decisiones en cuanto al pronóstico que presente el paciente.

Es vital que los médicos sepan utilizar este tipo de estudios a su favor para hacer la tarea de diagnosticar y tratar a sus pacientes con mayor eficacia y con un menor margen de error, además, esta herramienta puede ayudar a los pacientes a prevenir varios tipo de enfermedades y con ello disminuir la tasa de personas con padecimientos graves.

     Es por ellos que se debe tomar en cuenta la opinión de un profesional en la materia de bioestadistica para contrastar las ideas, proyectos que se planifican y asi tener un grado de seguridad en lo que se planteo para evitar la perdida de dinero, tiempo y esfuerzo.

Gracias a que la bioestadistica nos indica que los proyectos planteados son verdaderos y correctos podemos tener la certeza de lo que se plantea, además la estadística es una gran herramienta que ayuda a construir la ciencia, si la estadística es de gran calidad la ciencia será de gran calidad. 

La estadística se involucra en la ciencia para hacerle saber cuando estos datos están correctos o como puede mejorar sus métodos de investigación y así estos adquieran credibilidad. 

     En un país se debe tener conocimientos básicos sobre la estadística ya que permite tener una idea de distintas poblaciones, estadísticos en la sociedad, incluso una de las áreas con mayor aplicación a profundidad de la estadística es la farmacéutica con la finalidad de acreditar con valores reales arrojados por estadísticas aplicadas la calidad de sus productos farmacéuticos en el mercado.

La estadística es una profesión respetable academicamente y es indispensable tenerla en cuenta en la cualquier rama de la medicina 

Mejor bioestadística, mejor ciencia médica.

La estadística nace por el esfuerzo de los estados de allí viene la palabra estadística, se basa en entender a la sociedad, en conocerla mejor, es estudiar la poblaciones tomando en cuenta sus características (altos, bajos, hombres, mujeres).

La estadística tiene injerencia en la práctica profesional de disciplinas tan variadas como medicina, veterinaria, climatología, economía entre otras.

En cuanto a la demografía, se puede definir como la ciencia que tiene como objetivo el estudio de las poblaciones humanas y que trata de su dimensión, estructura, evolución y características generales, considerados desde un punto de vista cuantitativo. Por tanto la demografía estudia estadísticamente la estructura y la dinámica de la población y las leyes que rigen estos fenómenos.

La estadística muchas veces es una herramienta fundamental para responder a preguntas de cómo funcionan procesos sociales

La demografía y la estadística se complementan ya que para los demógrafos uno de los instrumentos fundamentales para la realización de sus estudios es el análisis de encuestas. 

Resumen. ULA Medicina.

Bioestadistica 

La bioestadistica es la aplicación de la estadística a los problemas biológicos. Estadística es el estudio científico de datos numéricos basados en fenómenos naturales.

Son muchas y distintas las definiciones que se han elaborado para este termino; es conveniente tener en cuenta varias de ella. Las siguientes son algunas de las definiciones mas conocidas:

- La estadística es la disciplina que se ocupa en el tratamiento de datos numéricos derivados de grupos de individuos.

- Es un método empleado en la toma de decisiones frente a la incertidumbre partiendo de datos numéricos y midiendo los riesgos en base a probabilidades.

La estadística se divide en:

-Estadística descriptiva: es aquella que hace una descripción completa de la muestra o población centrando la atención en sus distribución  frecuencia, tendencias. Cuando esta descripción es hecha sobre toda la población, recibe el nombre de Censo.

- Estadística Inferencial: es aquella que permite proyectar la información obtenida de una muestra a toda la población. 

Bioestadistica 

El primer médico que utilizo métodos matemáticos para cuantificar variables de pacientes y sus enfermedades fue el francés Pierre Charles Alexander Louis (1787-1872), en un estudio de la tuberculosis que influyo en toda una generación de estudiantes. Sus discípulos reforzaron la nueva ciencias de la epidemiologia con el método estadístico.

En la realización de cualquier estudio estadístico se parte de la existencia de una población dada, en términos sencillos, la poblacion es a Quien le vamos a indagar sobre un tema con propiedad comunes.
La población es el conjunto de elementos que cumplen ciertas propiedades comunes. Las poblaciones se definen según el campo de interés: 
-Población Finita: un numero fijo de valores
-Población Infinita: un numero indeterminado de valores.

Muestra
Es un subconjunto de la población que cumplen ciertas propiedades comunes.

Dato
Son cada uno de los elementos, individuos, cosas o entes abstractos que integran una muestra determinada.

Parámetro
Es un valor constante y especifico en cada población estadística y ayuda al investigador a tener una idea aproximada de la distribución poblacional de la característica de estudio.

Escalas de medición y variables estadísticas

Escala: es una sucesión ordenada por grado e intensidad, pero de la misma especie. Las principales son:

- Escala nominal: no se ordenan, son dicotomicas no ordenables.
- Escala ordinal: pueden clasificarse por grados según algún criterio. 
- Escala de intervalo: el valor de 0 (cero) NO indica la ausencia de la característica.
- Escala de razón: el valor de 0 (cero) indica la ausencia de la característica. 

Variables estadísticas
Es la característica o atributo que aun siendo común a todos los elementos de la población  esta sujeta a variaciones de uno u otro elemento. Se clasifican en:

-Variables cuantitativas: son todas aquellas variables susceptibles de medición.
Ejemplo: la cantidad de calorías que consume una persona al dia. 
 las variables cuantitativas se clasifican a su vez en: 
                - Variables cuantitativas continuas: son aquellas que pueden tomar infinitos valores en un intervalo.
                  Ejemplo: El largo del cabello de una persona.
                 - Variables cuantitativas discretas: son aquellas que no pueden tomar valores fraccionados en un intervalo dado. Ejemplo: El numero de glóbulos rojos en una muestra de sangre.

-Variables cualitativas: son todas aquellas variables que no son susceptibles de medición.
Ejemplo: la preferencia de un determinado alimento. 

Las variables cuantitativas se clasifican a su vez en: 
                - Variables cualitativas nominales: son aquellas que solo permiten dos clasificaciones o categorías. Ejemplo: El habito de fumar. (Fuma o no fuma)
                 - Variables cualitativas ordinal: son aquellas que permiten mas de dos clasificaciones o categorías. Ejemplo: Los tipos de carnes.

Variables en un experimento o investigación:
- Variable dependiente: no depende de otra, es el objetivo de la investigación.
- Variable Independiente: depende de otra variables.
-Variables intervinientes: pueden formar parte del estudio.

Planificación y ejecución de investigaciones medicas.

Planificación: tiene por finalidad el estudio de los detalles concernientes a la recolección, elaboración y análisis de la información, para estudiar cierto problema de investigación Considerando: tiempo, personal, presupuesto.

Pasos para la planificación:
1. Planteamiento del problema. 
2. Búsqueda y evaluación de la información existente. 
3. Formulación de hipótesis. 
4. Verificación de las hipótesis. 
5. Conclusiones y Recomendaciones.

• 1. Planteamiento del problemas: Explicar ¿Que? vamos a estudiar, estableciendo de manera clara el problema que se trata de investigar. 

• Determinacion de los objetivos: cuando determinamos el objetivo final, significa las posibilidades de aplicación práctica de la investigación, es decir, explicar PARA QUÉ se realiza.

• Objetivos inmediatos: se explica CÓMO se va hacer la investigación, es decir, se señala la estrategia y los procedimientos generales que se usarán en el desarrollo de la misma.

• 2. Búsqueda y evaluación de la información existente: el investigador debe revisar, en cuanto sea posible, lo que al respecto se haya hecho, con el fin de percatarse de lo que realmente se conoce del problema y familiarizarse con las técnicas de investigación más convenientes para el objeto del estudio.

• 3. Formulación de la hipótesis

• Es aquella que permite centrar la observación sobre aquellos fenómenos que guardan relación con el problema que se estudia, evitando que muchos hechos importantes pasen inadvertidos o que el investigador se pierda en un cúmulo de observaciones inconexas.. Es fundamental que la formulación se realice de manera clara, ya que la planificación y ejecución de la investigación dependerá de la hipótesis a probar.

• 4. Verificación de la hipótesis
• -Planeamiento y ejecución de encuestan: metodológico, ejecución.

• 5. Conclusiones y recomendaciones